Matrix
Techniques in Optics
Transfer
Matrix for a Series of Elements
The power of the matrix technique becomes evident when you realize that the transfer matrix for a series of optical elements is simply the product of the transfer matrices for the individual elements. For example, suppose we have two drift spaces following each other - first followed by . The combined transfer matrix should look like that for a drift space of length . Check it out:
On the L.H.S. of the above equation, the transfer matrix for the first drift space is to the right of the transfer matrix of the second drift space. This sets the order in which you define the elements. The element that operates first has its matrix in the rightmost place in the product of matrices.
Suppose we have a curved surface of radius R1 followed by a drift space of thickness t followed by a curved surface of radius -R2. This would describe a 'thick lens'. We go from air to glass to air. The total transfer matrix would look like:
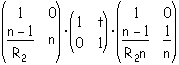
If we take t = 0, we have a 'thin lens' and this reduces to:
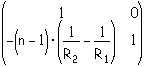
which is the transfer matrix for a thin lens with: