Matrix
Techniques in Optics
Some
Mathematical Relations for Matrices
This is a reminder of some relations you undoubtedly learned about in linear algebra. Our problem is made more simple because all of the matrices we will be dealing with are 2-dimensional. Suppose we have two matrices:
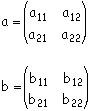
Then you are reminded that:
and the multiplication is not necessarily commutative. If k is a scalar and a is a matrix then ka multiplies each element of matrix a by the same scalar. The determinant of matrix a is written as:
and we have:
If the determinant of a matrix is zero, the matrix is said to be singular. If the determinant of the matrix is unity, the matrix is said to be unimodular. Note that the transfer matrices for the drift space and thin-lens are unimodular.
Consider the matrix:
The inverse of the matrix times the matrix yields the unit matrix. For a two-dimensional matrix, finding the inverse is a snap. Here's the recipe:
Note that we negate the off-diagonal elements, flip the diagonal elements and then divide by the determinant. Here's why this works:
![]()