Suppose now that our damped hamronic oscillator is subject to a driving force which is harmonic. In particular, we will assume that now the differential equation is:
where the subscript d indicates the driving frequency. We already solved this equation with the R.H.S. = 0. We found an exponentially (with time) damped solution. So after a sufficiently long time, that solution goes to zero. But we're still left with the driving term. We'll assume a solution of the form:
So now we need to find C and the phase angle. Putting this solution into the deifferential equation, we get:
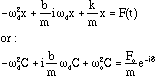
where we divided through by
![]() to get to the last step.
to get to the last step.
Remembeting Euler's equation and that we need to consider the real and imaginary parts separately:
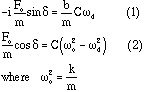
First divide (1) by (2). Then square (1) and (2) and add. This gets you the following:
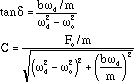
Our solution (the steady state solution - after the exponentially damped one has died away) oscillates with the same frequency as the driving force. But is is out of phase with the driving force and the maximum amplitude is reached when the driving force oscillates with a frequqncy equal to the natural frequency (resonance). You may want to look at plots of the phase and amplitude.